Steepest Descent Optimization with Optimal Step Size (Wolfe) and Newton’s Method Demo in Python
November 2020  –  Me

Overview:
I l0ve math, and was really excited to learn about optimization algorithms.
This google colab sheet demonstrates steepest decent algorithms using numeric approximation.

Tools:
Numpy: matrix operations
Matplotlib: viz

Language used: Python

See my demo here. :-D

Here’s a preview:
for function f(x,y) = (x+1)^2 + 8y^2 - 3x - y + 1

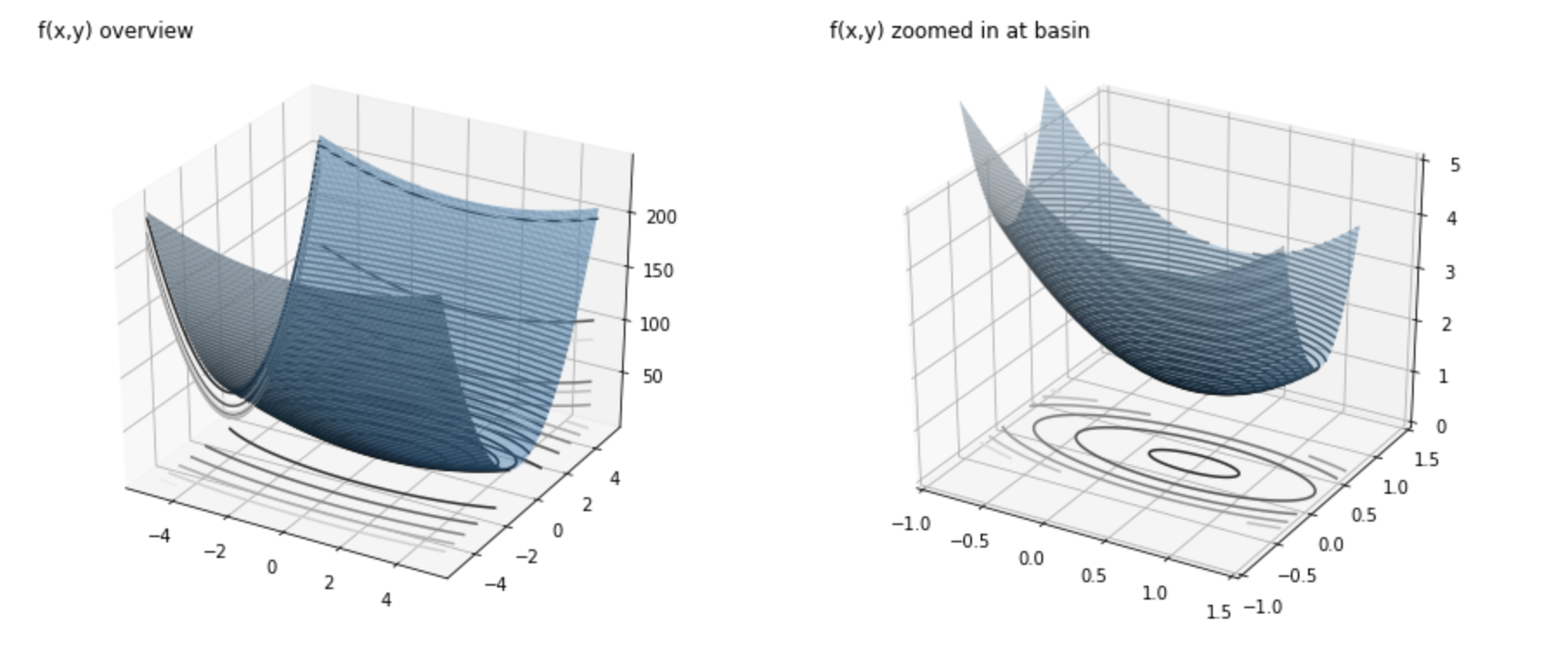
Steepest descent using optimal step size:

def f(x, y):
    return (x+1)**2 + 8*y**2 - 3*x - 3*y + 1

# Initiate Q and grad_f defined by given function
def Q():
    return np.array([[2, 0], [0, 16]])


def grad_f(x_k, y_k):
    # returns gradient of f at xv_k
    return np.array([[2 * x_k - 1], [16 * y_k - 1]])

# calculates dot products
def dot_prod(a, b):
    # computes the dot product of vectors a and b
    if len(a) != len(b):
        print("DOT PROD NOT DEFINED")
    else:
        prod = 0
        for i in range(len(a)):
            temp = a[i] * b[i]
            prod = prod + temp
    return prod


# steepest descent algorithm

def alpha(x_k, y_k):
    return dot_prod(grad_f(x_k, y_k), grad_f(x_k, y_k)) / dot_prod(grad_f(x_k, y_k), np.matmul(Q(), grad_f(x_k, y_k)))

def xv_k_1(x_k, y_k):
    a_k = alpha(x_k, y_k)
    grad_f_x_k, grad_f_y_k = grad_f(x_k, y_k).T[0]
    x_k_1 = x_k - a_k * grad_f_x_k
    y_k_1 = y_k - a_k * grad_f_y_k
    return np.array([x_k_1, y_k_1])

def steepest_desc(x_0, y_0):
    # arrays to store descent progress at each k
    X, Y = [x_0], [y_0]

    epsilon = 10 ** (-6)

    for k in range(10 ** 4):  # i want to stop after at most k = 10**4-1
        if np.linalg.norm(grad_f(X[len(X) - 1], Y[len(Y) - 1])) >= epsilon:
            next_X, next_Y = xv_k_1(X[len(X) - 1], Y[len(Y) - 1]).T[0]
            X.append(next_X)
            Y.append(next_Y)
        else:
            break
    return [len(X), X, Y]

# investigate convergence speed
min_point = np.array([0.5, 1 / 16])
starting_dist_from_min = []
x_0_list = []
y_0_list = []
steps_list = []
for x_0 in range(-5, 6):
    for y_0 in range(-5, 6):
        start = np.array([x_0, y_0])
        steps = steepest_desc(x_0, y_0)[0]
        starting_dist_from_min.append(np.linalg.norm(start - min_point))
        steps_list.append(steps)
        x_0_list.append(x_0)
        y_0_list.append(y_0)
        print("steps =", steps, "  start: (", x_0, y_0, ")")